Topic 7: The Second Law of Thermodynamics and Entropy#
Introduction#
In Section The Carnot cycle: the ‘perfect’ heat engine we said that no heat engine can possibly be more efficient than a Carnot engine, and in Section Introduction we said that when we place two bodies of different temperature in thermal contact, heat flows from the hotter body to the cooler body. These are, in fact, two statements of the Second Law of Thermodynamics:
In other words, heat does not flow spontaneously from cold to hot.
There is also a third statement of the Second Law:
The Clausius and Kelvin statements of the Second Law are in fact precisely equivalent, though this is not obvious at first glance, and the Carnot statement can be proved from the Clausius statement. Notice that both the Clausius and the Kelvin statements imply an arrow of time: if we were to consider a time-reversed version of Clausius statement, we would see heat flowing from the hotter body to the cooler, which is perfectly legitimate, and likewise a time-reversed version of the Kelvin statement would involve the complete conversion of work into heat, which is also legitimate.
Equivalence of the Clausius and Kelvin statements of the Second Law#
In order to prove that two statements A and B are equivalent, we need to prove that A implies B and B implies A. If that is the case, then whenever A is true, B is true, and vice versa, so thy are equivalent. For the Clausius and Kelvin statements, we can prove both implications by contradiction.
Clausius implies Kelvin#
Suppose that Claus’ statement is true but Kelvin’s is not. If Kelvin’s statement is not true we can build an engine K that converts heat into work. We connect this to a Carnot engine working in reverse as shown in Fig. 19.
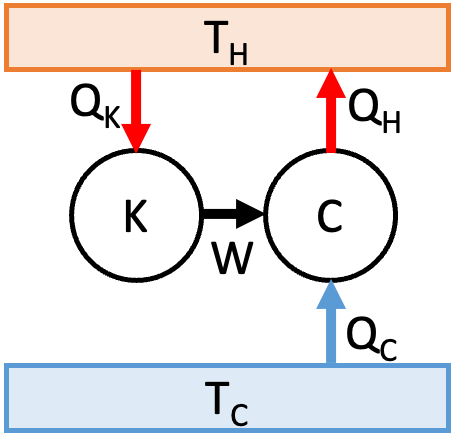
Fig. 19 If Kelvin is false, so is Clausius.#
By the First Law, \(W = Q_K\) and also \(W = Q_{H} - Q_{C}\). Therefore \(Q_C{} = Q_{H} - Q_{K}\). Therefore the composite engine has the effect of taking heat \(Q_C\) from the cold reservoir and transferring it to the hot reservoir. But this is in violation of Clausius’ statement, which contradicts our initial assumption. Therefore, Clausius’ statement implies Kelvin’s statement.
Kelvin implies Clausius#
We can use the same approach here. Assume that Clausius’ statement is not true, and that we can therefore build a machine that simply transports heat \(Q_{C}^{'}\) from a cold reservoir to a hot reservoir. Connect this to a Carnot engine running forwards, which takes heat \(Q_{H}\) from a hot reservoir, does work \(W\), and rejects heat \(Q_{C}\). If we adjust the Clausius machine so that \(Q_{C} = Q_{C}^{'}\), then the combined engine takes in heat \(Q_{H} - Q_{C}\) and converts it completely to work, which violates Kelvin’s statement. Therefore, if Kelvin’s statement is true, Clausius’ statement must also be true.
Clausius implies Carnot#
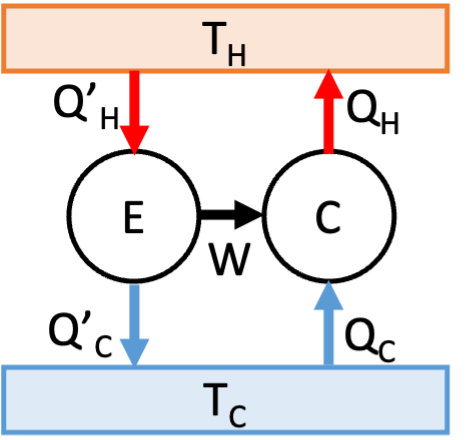
Fig. 20 Clausius’ statement implies Carnot’s.#
Assume that Carnot’s statement is not true, and we can therefore build an engine \(E\) that has a higher efficiency than a Carnot engine. We connect this super-efficient engine to a Carnot engine running in reverse, as shown in Fig. 20. Engine \(E\) takes in heat \(Q_{H}^{'}\), does work \(W\), and ejects heat Q\(_{C}^{'}\); the Carnot engine takes in heat \(Q_{C}\) and the work done by engine \(E\), and ejects heat \(Q_{H}\). Since \(\eta = W/Q_{H}\), and we have assumed that \(\eta_{E} > \eta_{C}\), it follows that \(Q_{H}^{'} < Q_{H}\). The First Law tells us that
(taking all the \(Q\)’s to be positive). Therefore \(Q_{C}^{'} < Q_{C}\) and the net effect of the combined engine is to take heat \(Q_{C} - Q_{C}^{'}\) from the cold reservoir and eject it into the hot reservoir, which violates Clausius’ statement, Therefore Clausius’ statement of the Second Law implies that engine \(E\) cannot exist.
The Third Law of Thermodynamics#
If we could run a Carnot engine with its cold reservoir at 0 K, we could violate Kelvin’s statement, because such an engine would have \(\eta\) = 1, and would therefore convert all the input heat into work. This is forbidden by the Third Law of Thermodynamics, Nernst’s statement of which is
Entropy#
From the Carnot cycle definition of thermodynamic temperature, Equation (36), we know that \(\frac{|Q_{H}|}{T_{H}} = \frac{|Q_{C}|}{T_{C}}\). Accounting properly for the signs, i.e. recognising that \(Q_{C} < 0\), we also have
We can generalise this sum to an integral around a closed loop (imagine lots of mini Carnot cycles working between temperatures \(T\) and \(T+dT\), all satisfying Equation (41)):
This holds only if the loop consists entirely of reversible processes, which is why we put the label ‘rev’ in the \(\bar{d}Q\).
It follows from this that the quantity \(\bar{d}Q_{\rm rev}/T\) is an exact differential, i.e. the value of the integral between two states A and B is independent of the path taken.

Fig. 21 Two arbritrary paths between states A and B#
To see this, consider states A and B in Fig. 21. The two paths connecting A and B are both reversible. We can integrate from A to B along path 1 and get \(\Delta S_{1} = \int_{1} \frac{\bar{d}Q}{T}\), or we can integrate along path 2 and get \(\Delta S_{2} = \int_{2} \frac{\bar{d}Q}{T}\). But we can also reverse the direction of path 2, since we have defined it to be reversible, and integrate from B to A, which must give us \(\int_{-2} \frac{\bar{d}Q}{T} = - \int_{2} \frac{\bar{d}Q}{T} = -\Delta S_{2}\), where the minus sign indicates that path 2 is taken in reverse.
Now, if we integrate from A to B via path 1, and then from B to A via path 2, we have completed a closed reversible cycle, and Eqn (42) tells us that
Therefore since paths 1 and 2 were arbitrary, we must have
for any reversible path. Therefore \(\bar{d}Q_{\rm rev}/T\) is an exact differential. It follows that the quantity \(S\) defined by
is a function of state. We call \(S\) the entropy of the state.
This definition only allows us to calculate changes in entropy, \(\Delta S\); if we try to calculate the absolute value of \(S\) we have an undetermined integration constant. To calculate absolute values of \(S\) we need a microscopic definition in terms of individual particles. you will meet this definition (and show that it is equivalent to the definition in Eqn (42)) when you study statistical mechanics next year.
Entropy and the First Law#
We can write Eqn (42) as \(T dS = \bar{d} Q_{\rm rev}\). If we also assume that we are dealing with an ideal gas, such that \(\bar{d}W = -P dV\), we can write the differential form of the First Law as
But now a miracle has occurred: everything in Eqn (44) is a function of state, and therefore Eqn (44) holds irrespective of the path taken. This can be very useful: if you want to calculate \(\Delta U\) for an irreversible process, and you know the start and end states, you can apply Eqn (44) to any reversible path between the start and end states and the result will be the same as for the irreversible process. (This doesn’t mean that the heat supplied and the work done will be the same: \(\bar{d}Q\) and \(\bar{d}W\) are still inexact differentials. But the changes in internal energy, entropy and volume will be the same.)
Entropy in reversible and irreversible processes#
So far we have considered entropy in the context of reversible processes. What about irreversible processes?
Irreversible processes are irreversible because energy has dissipated in a way that cannot be reversed .e.g friction. This is clearly not work: as we noted in Section 1, work is energy transfer associated with ordered motion, and is therefore reversible. Hence, if we suppose that the maximum work that can be extracted from a reversible transition between state A and state B is \(W_{\rm rev}\) (i.e. \(\Delta U = Q - W_{\rm rev}\), since we’ve defined \(W_{\rm rev}\) as work done by the system), we expect that an irreversible transition between the same two states will extract work \(W_{\rm irr} < W_{\rm rev}\).
If we make this transition infinitesimal, such that states A and B are very close together, we can write
(again, recall that the minus sign here is because the work is done by, not on, the system). So we have
This emphasises that the definition of \(S\) refers to the heat supplied in a reversible process. If you have an irreversible process, the definition \(dS = \bar{d}Q/T\) does not apply. This means that if we wish to calculate the entropy change associated with an irreversible process, we cannot simply integrate \(\bar{d}Q/T\). Fortunately, there is a solution to this, because entropy is a function of state: if we can define a reversible path with the same initial and final state, we can use this to calculate \(\Delta S\).
Example 7.1
Suppose that we connect a small system with temperature \(T_{S}\) to a very large heat reservoir with temperature \(T_{R}\). The two will reach equilibrium at temperature \(T_{R}\) (we assume that the heat transfer to or from the small system has negligible effect on the temperature of the reservoir). What is the change in entropy (i) of the small system; (ii) of the large reservoir; (iii) of the Universe? Assume that the volume of the small system does not change, and that the combined system of the small system plus the reservoir is thermally isolated from the rest of the Universe.
This is an irreversible process, since reversing it would require heat to flow from cold to hot without doing any work, which contravenes the Second Law. However, we can replace it with a reversible transfer of heat at constant temperature for the reservoir, and constant volume for the small system.
The heat transferred to or from the small system is \(\Delta Q_{S} = C_{V} (T_{R} - T_{S})\),m where \(C_{V}\) is the heat capacity of the small system at constant volume. \(\Delta Q_{S}\) is positive if the small system was initially cooler than the reservoir (heat is supplied to the small system) and negative if the small system was initially warmer (heat is lost from the small system). Since the combined system is thermally isolated and no work is being done, we must have \(\Delta Q_{R} = - \Delta Q_{S}\).
As the reservoir is at constant temperature throughout, the entropy change is \(\Delta S_{R} = \frac{\Delta Q_{R}}{T_{R}} = - \frac{C_{V} (T_{R} - T_{S})}{T_{R}} = C_{V} \left( \frac{T_{S}}{T_{R}} - 1\right)\). For the small system, \(dS = \bar{d}Q/T = C_{V} dT/T\). We can integrate this from \(T_{S}\) to \(T_{R}\): \(\Delta S_{S} = \int_{T_{S}}^{T_{R}} \frac{C_{V} dT}{T} = C_{V} \ln \left( \frac{T_R}{T_S} \right)\). The total entropy change is \(\Delta S_{\rm tot} = C_{V} \left( \ln \left( \frac{T_R}{T_S}\right) + \frac{T_S}{T_R} - 1 \right)\).
There are various points to note here
Although the temperature of the reservoir does not change, its entropy does.
Although the heat flow into or out of the two subsystems is the same (apart from the sign), the entropy change is not.
\(\Delta S_{\rm tot}\) is always greater than zero if \(T_{\rm R} \neq T_{S}\).
Point 3 is illustrated in Fig. 22. We can also deduced it by differentiating the above expression for \(\Delta S_{\rm tot}\). If we write \(r = T_{R} / T_{S}\), we have \(\frac{d (\Delta S_{\rm tot})}{dr} = C_{V} \left( \frac{1}{r} - \frac{1}{r^2} \right)\), which is equal to zero when \(r = 1\) at which point \(\Delta S_{\rm tot} = C_{V} (\ln (1) + 1 - 1) = 0\). This must be a minimum, because the derivative is positive (curve rising) for \(r > 1\) and negative (curve falling) for \(r < 1\). Hence \(\Delta S_{\rm tot} \leq 0\) for all values of \(T_{R}/T_{S}\), and is zero only if \(T_{R} = T_{S}\) and there is no heat flow.
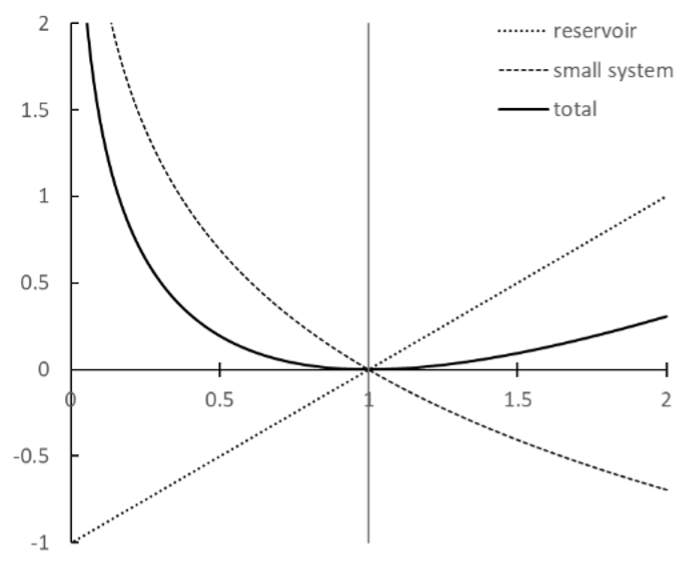
Fig. 22 Entropy changes for example 7.1#
In the above example, the entropy change of the small system is negative when the system cools to equilibrium, and positive when it warms, as we would expect since the heat flow is negative when it cools (heat is transferred from the small system) and positive when it warms (heat is transferred to the small system). However, the total change in entropy, taking the surroundings into account, is always positive (except in the case where the two systems were already in equilibrium before being brought into contact). In contrast, if we have a reversible process, the entropy change in the surroundings will always balance the entropy change in the small system.
This is necessary so if the process is quasistatic, since - by definition - we are assuming in a quasistatic process that the system is essentially in equilibrium with its surroundings, i.e. at the same temperature. So, if the system receives heat \(\bar{d}Q_{\rm rev}\) from its surroundings at temperature \(T\), its entropy change is \(dS_{\rm sys} = \bar{d}Q_{\rm rev}/T\) and the entropy change of the surroundings is \(dS_{\rm surr} = -\bar{d}Q_{\rm rev}/T\).
This leads to yet another statement of the Second Law
Note the key qualifier: not just any system, but a thermally isolated system. If the system is not thermally isolated, by definition heat can flow into and out of the system, and this will be accompanied by a change in entropy, which can be positive or negative. This explains why we see many processes in nature, e.g. crystal growth, which appear to be associated with a decrease in entropy: in such cases the entropy of the system may indeed decrease, but it is not a thermally isolated system, and the decrease is compensated by an increase in the entropy of the surroundings, as in Example 7.1
The Universe is the ultimate thermally isolated system, so the entropy statement of the Second Law implies that the entropy of the Universe cannot decrease.
Example 7.2
Calculate the entropy change in the system and its surroundings for each stage of a Carnot cycle (Topic 6).
A Carnot cycle consists of 4 stages (i) isothermal compression at \(T_{C}\); (ii) adiabatic compression increasing the temperature to \(T_{H}\); (iii) isothermal expansion at temperature \(T_{H}\); (iv) adiabatic expansion decreasing the temperature back to \(T_{C}\).
We can do the adiabatic steps 2 and 4 immediately: by definition, in an adiabatic process no heat is transferred, so \(\Delta S_{\rm sys} = \Delta S_{\rm surr} = 0\).
In step 1 work is done on the gas, but the internal energy of the gas does not change (in an isothermal process \(\Delta U = 0\)), so heat must be expelled by the gas, hence \(Q < 0\). The entropy change of the system is \(\Delta S_{\rm sys} = -|Q_{C}|/T_{C}\) (we do not need to do an integration because the temperature is constant). Conversely, the surroundings (the cold reservoir) receive heat \(|Q_{C}|\), so the entropy change is \(\Delta S_{\rm surr} = |Q_{C}|/T_{C}\).
In step 3, work is done by the gas, so it must take in heat (\(Q > 0\)). The entropy change of the system is \(\Delta S_{\rm sys} = Q_{H}/T_{H}\), and the entropy change of the surroundings (the hot reservoir) is \(\Delta S_{\rm surr} = -Q_{H}/T_{H}\). But from Eqn (36) we know that \(Q_{H}/T_{H} = |Q_{C}|/T_{C}\), and so we can write these as \(\Delta S_{\rm sys} = |Q_{C}|/T_{C}\) and \(\Delta S_{\rm surr} = -|Q_{C}|/T_{C}\).
From this we see that (1) the total entropy change of the system is zero, as it must be, since this is a closed cycle and entropy is a function of state; (2) the entropy change of system plus surroundings is zero not for the cycle as a whole, but also for each individual step. This is what we would expect for reversible processes.
Example 7.3
A Carnot engine takes 2000 J of heat from a reservoir at 500 K, does some work, and discards some heat to a reservoir at 350 K. (a) How much heat is discarded? (b) How much work is done? (c) What is its efficiency? (d) What is the total entropy change?
(a) The heat discarded is \(|Q_{C}| = Q_{H}\frac{T_{C}}{T_{H}} = 2000 \frac{350}{500} = 1400\) J
(b) Work done \(|W| = Q_{H} - |Q_{C}| = 2000 - 1400 = 600\) J
(c) Efficiency of a Carnot engine is \(\eta = 1 - T_{C}/T_{H} = 1 - \frac{350}{500} = 0.3\)
(d) There is no change in entropy during adiabatic compression or expansion (\(Q = 0\)).
During the isothermal expansion the engine takes in 2000 J of heat so \(\Delta S_{H} = \frac{Q_{H}}{T_{H}} = 4\) J/K.
During the isothermal compression the engine gives off 1400 J of heat so \(\Delta S_{C} = \frac{Q_{C}}{T_{C}} = -4\) J/K
so the net change in entropy is \(\Delta S_{total} = \Delta S_{H} + \Delta S_{C} = 0\) (the sum of the entropy changes is zero since uniquely all processes are reversible in the Carnot cycle, in contrast to Otto, Diesel etc)
Example 7.4
Heat from a very massive body at 25\(^{\circ}\) C is added to 0.35 kg of ice at 0.0\(^{\circ}\) C until it is all melted. (a) What is the change in entropy of the water? (b) What is the change in entropy of the massive body? (c) What is the total change in entropy of the water and heat source? (d) Compare your answer to part (a) with the change in entropy of water at 100\(^{\circ}\) being vaporized and convered to steam at 100\(^{\circ}\) C. Interpret your answer in the context of entropy being a measure of the randomness of a system.
(a) The latent heat of fusion of water is \(L_{f} = 3.34 \times 10^{5}\) J/kg (Table 4 in Topic 2), so \(Q = 0.35 \times 3.34 \times 10^{5} = 117\) kJ and \(\Delta S_{C} = Q/T_{C}\) = \(1.17 \times 10^{5}/273 = 428\) J/K.
(b) \(\Delta S_{H} = Q/T_{H} = -1.17 \times 10^{5}/298 = -393\) J/K.
(c) \(\Delta S_{total} = 428 - 393 = 36\) J/K.
(d) The latent heat of vaporization is \(L_{v} = 2.26 \times 10^{6}\) J/kg (Table 4 in Topic 2), so \(Q = 0.35 \times 2.26 \times 10^{6} = 791\) kJ and \(\Delta S = Q/T = 7.91 \times 10^{5}/373 = 2.12\) kJ/K, five times greater than melting ice (steam is much more disordered than liquid water).
Example 7.5
Suppose 1.0 kg of water at 100\(^{\circ}\) C is placed in thermal contact with 1.0 kg of water at 0\(^{\circ}\) C. What is the total change in entropy? Assume a constant 4190 J/kg/K heat capacity of water.
Since equal amounts of hot (H = 373 K) and cold (C = 273 K) water are combined, the equilibrium temperature is 323 K. The entropy change is \(\Delta S = \Delta Q/T = mc \int_{T_{1}}^{T_{2}} \frac{dT}{T}\) so the entropy changes of hot water (\(\Delta S_{H}\)) and cold water (\(\Delta S_{C}\)) are
\(\Delta S_{H} = (1.0) (4190) \ln (323/373) = -603\) J/K and \(\Delta S_{C} = (1.0) (4190) \ln (323/273) = +705\) J/K.
So the total change in entropy is \(\Delta S_{\rm total} = \Delta S_{H} + \Delta S_{C} = +102\) J/K. There is an increase in entropy since the heat flow is irreversible. Entropy increases continually as the two liquids come into equilibrium.
Entropy as a measure of disorder#
Total entropy increases in irreversible processes, but is zero in reversible processes. We saw that what makes a process irreversible is the dissipation of energy - in essence, some of the energy that would, in a reversible system, be released as work (ordered motion) is instead dissipated in some disordered fashion. Also, the entropy of a system increases when heat flows into it, and decreases when heat flows out of it, and we saw that heat is energy associated with disordered (i.e. random) motion. These observations suggest that entropy is in some way associated with disorder. This is indeed true, and you will explore the microscopic definition of entropy next year.
