Topic 1: Temperature and Thermal Equilibrium

Introduction

You know from everyday experience that when a hot object (at high temperature) is brought in contact with a cold one (at low temperature), the hot object will get cooler and the cold object warmer until eventually there is no flow of heat from one to the other. When there is no flow of heat, the objects have reached thermal equilibrium.

But what is temperature? On a microscopic level, temperature is related to the kinetic energy of the atoms/molecules. The atoms have thermal energy and move around randomly. The higher the average kinetic energy of the atoms, the higher the temperature.

Zeroth law of thermodynamics

It’s called the zeroth law because it is more fundamental than the first law, but was defined later. Early thermak physicists took this property for granted, as being obviously true (thermometers do, empirically, work), but it is necessary to state it formally so as to have a clear definition of the concept of temperature.

The zeroth (0th) law of thermodynamics states that

If a body A is in thermal equilibrium with body C, and body B is in thermal equilibrium with body C, then body A is in thermal equilibrium with body B.

i.e. if two systems are each in thermal equilibrium with a third then they are in thermal equilibrium with each other. This allows us to introduce the concept of temperature: bodies that are in thermal equilibrium with each other have the same temperature. Taken together with observations of heat flow, it also lets us define a relative temperature scale: if heat flows from A to B when they are placed in contact, then A is at a higher temperature than B.

Measuring temperature

From the zeroth law of thermodynamics we know that if two systems each have the same temperature as a third then they have the same temperature as each other. We can then use that third system as a reference to measure temperature against, i.e. we can use it as a thermometer. To measure temperature, we need an instrument (thermometer), a scale and a standard. Anything that changes its physical behaviour with temperature can be used as a thermometer: for example, thermal expansion of a liquid, bending of a bimetallic strip, electrical resistance of a metal, frequency of the peak intensity of emitted electromagnetic radiation. We can set up a temperature scale by defining the temperature at two fixed reference points - for example, the Celsius or Centigrade scale is defined by stating that the freezing point of pure water at one atmosphere pressure is 0\(^{\circ}\) C, and the boiling point is 100\(^{\circ}\) C. If we have an instrument with a property \(X(T)\) that depends on temperature, we can then define the temperature of any object in degrees Celsius by

(1)\[\begin{align} T(X) = 100 \frac{X - X_{0} }{ X_{100} - X_{0} } \end{align}\]

where \(X_{100}\) is the value of \(X\) at 100\(^{\circ}\) C and \(X_{0}\) is the value at 0\(^{\circ}\) C.

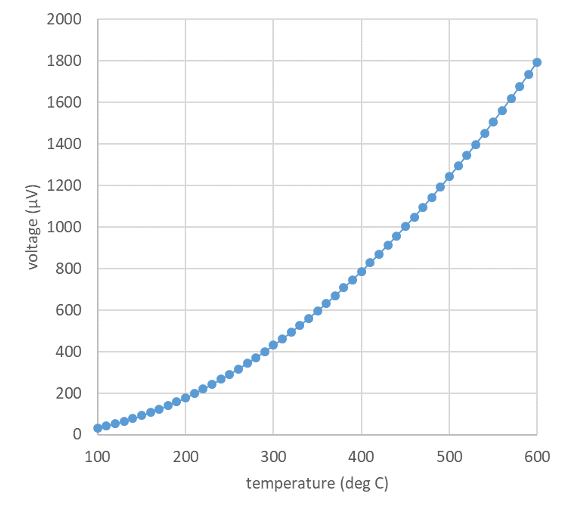
Fig. 1 Calibration curve of a thermocouple, using data from the NIST engineering statistics handbook

The problem with this system is that although we have guaranteed that all thermometers will agree with each other at 0\(^{\circ}\) C and at 100\(^{\circ}\) C, we have not guaranteed that they will agree at any other temperature. This is because Equation (1) defines a scale that is linear in \(X\) (e.g. a temperature of 50\(^{\circ}\) C corresponds to a value of X exactly halfway between \(X_{0}\) and \(X_{100}\)), but many properties that vary with temperature do not do so linearly. For example, Fig. 1 shows the calibration curve of a thermocouple, which is a device that measures temperature by measuring the voltage generated across a junction of two dissimilar metals. It is clear that the voltage corresponding to 200\(^{\circ}\) C is not simply twice the voltage corresponding to 100\(^{\circ}\) C, as it should be according to Equation (1).

To solve this problem, we need to define some sort of reference scale, and then calibrate our thermometers with respect to that scale. We will see later in the course that the ideal gas law \(PV = nRT\) can provide such a reference scale: we can either maintain the gas at constant volume and measure how the pressure changes when we change the temperature, or maintain it at constant pressure and measure the volume change.

The ideal gas law predicts that the gas pressure at constant volume (or volume at constant pressure) should reach zero at T = 273.15\(^{\circ}\) C. This is defined as absolute zero. The Kelvin temperature scale takes absolute zero as one of its reference points and the triple point of water, i.e. the temperature at which ice, liquid water and water vapour all coexist in equilibrium, as the other. The triple point of water occurs at a pressure of 611.657 Pa and is defined to have a temperature of 273.16 K (see Fig. 2). Note that the advantage of the triple point over freezing and boiling points is that you do not have to specify (and measure) a pressure, since the triple point is a point (not a line) on the plot of pressure against temperature. Therefore, using a gas thermometer, we can define the Kelvin temperature of any object as

(2)\[\begin{split}\begin{align} T = T_{\rm triple} \frac{P(T)}{P_{\rm triple}} ({\rm const}. V) \\ T = T_{\rm triple} \frac{V(T)}{V_{\rm triple}} ({\rm const}. P) \end{align}\end{split}\]

Any other thermometer can be calibrated against a gas thermometer, or against any thermometer whose temperature dependence is based on well-defined and well-understood physics. Such thermometers are known as primary thermometers: besides constant-volume and constant-pressure gas thermometers, they include acoustic thermometers, which measure the speed of sound in a gas (which has a known relation to the average speed of gas molecules, and therefore to the temperature) and Johnson noise thermometers, which measure the electronic noise power across a resistor (this is generated by the random thermal motion of the charge carriers, and therefore is directly proportional to absolute temperature).

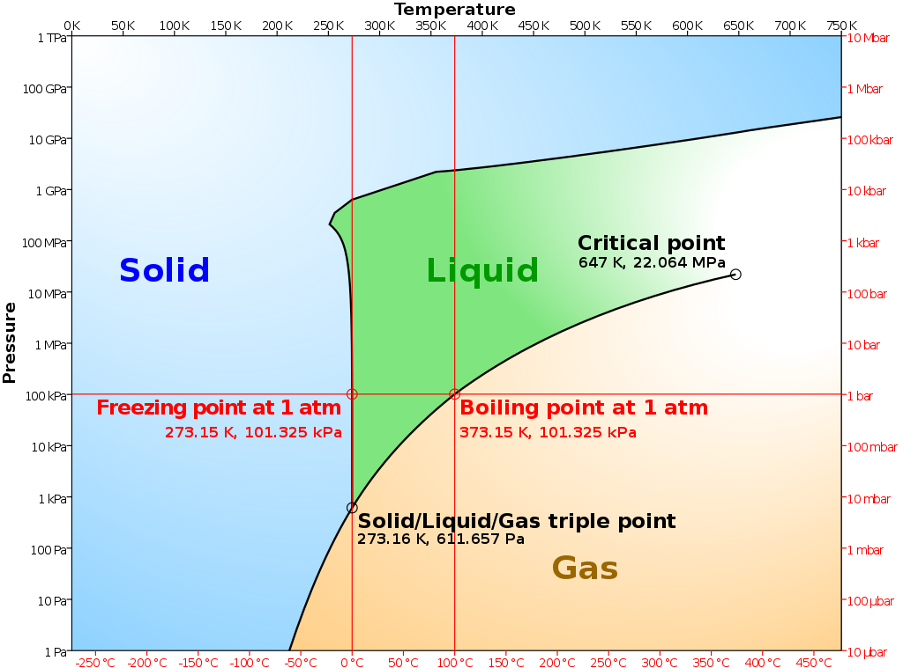
Fig. 2 align: center Phase diagram of water illustrating the triple point of water (ice, liquid water and water vapour coexist). Source: Wikipedia

Thermal expansion

Generally materials expand (increase in volume) on heating and contract (decrease in volume) on cooling. For small changes in temperature, the relationship is linear: the change in volume is proportional to the change in temperature. If we only measure the length of an object, the change in length corresponding to a change in temperature is given by

(3)\[\begin{align} \Delta L = \alpha L_{0} \Delta T, \end{align}\]

where \(L_0\) is the original length of the object and \(\alpha\) is the coefficient of linear expansion, which is a property of the material. The dimensions of alpha are inverse temperature, but its numerical values are often quoted in units such as \(\mu\)m/m/K for convenience.

If the material expands in three dimensions, the change in volume is given by a similar expression

(4)\[\begin{align} \Delta V = \beta V_{0} \Delta T, \end{align}\]

where \(V_{0}\) is the original volume and \(\beta\) is the coefficient of volume expansion.

If the material is isotropic, i.e. its properties are the same in all directions, we can derive a simple relationship between \(\alpha\) and \(\beta\). Consider a cube of the material, with volume \(V_0 = L_0^{3}\). Then the rate of change of volume with respect to temperature is given by

\[ \frac{dV}{dT} = 3 L^{2} \frac{dL}{dT} \]

by the chain rule. But from Equation (3), \(dL/dT = \alpha L_0\) and from Equation (4) \(dV/dT = \beta V_0\). If we substitute these in, we get

\[ \beta V_{0} = \beta L_{0}^{3} = 3 L_{0}^{2} \alpha L_{0} = 3 \alpha L_{0}^{3}, \]

from which we immediately read off

(5)\[\begin{align} \beta = 3 \alpha. \end{align}\]

Table entries from Table 17.2 of University Physics with Modern Physics (Pearson)

Table 1 Coefficients of volume expansion

Material	\(\beta\) K\(^{-1}\)
Aluminium	\(7.2 \times 10^{-5}\)
Copper	\(5.1 \times 10^{-5}\)
Steel	\(3.6 \times 10^{-5}\)
Mercury	\(1.8 \times 10^{-4}\)

Because thermal expansion is easy to measure and fairly linear with temperature, it is often used in thermometry. The most obvious example is the standard mercury-in-glass or alcohol-in-glass thermometer. Bimetallic strips, made of two strips of metal with different coefficients of thermal expansion bonded together along their long edges, bend when heated and can be used either as a thermometer (the bending moves a pointer on a scale) or as a heat-operated switch (the bending makes or breaks an electrical contact).

Example 1.1

Question

A mercury thermometer has a cylindrical bulb 2 cm in length and 0.8 cm in diameter, attached to a cylindrical tube 0.30 mm in diameter and 15 cm in length. The coefficient of linear thermal expansion of mercury is 61 \(\mu\)m/m/K. By how much does the mercury rise up the tube for a change in temperature of 1\(^{\circ}\) C?

Solution

The volume of the mercury in the bulb is \(\pi r^2 L = 1.01\) cm\(^{3}\) and we can neglect the volume in the tube (the largest it could possibly be is 0.01 cm\(^{3}\). The coefficient of linear expansion is \(61 \times 10^{-6}\) K\(^{-1}\), but we need the coefficient of volume expansion, so we use Equation (5) to get \(183 \times 10^{-6}\) K\(^{-1}\). Therefore the volume of the mercury increases by \(1.85 \times 10^{-4}\) cm\(^{3}\) for a temperature rise of 1 K. This must go up the tube, which has a cross-sectional area of \(\pi r^{2} = 7.07 \times 10^{-4}\) cm\(^{2}\). The mercury rises by \(1.84 \times 10^{-4} / 7.07 \times 10^{-4}\) = 0.26 cm.

Example 1.2

Question

A 200 cm\(^{3}\) glass flask is filled to the brim with mercury at 20\(^{\circ}\) C. How much mercury overflows when the temperature of the system is raised to 100\(^{\circ}\) C? The coefficient of linear expansion of the glass is \(0.40 \times 10^{-5}\) K\(^{-1}\).

Solution

From Equation 5, \(\beta_{\rm glass} = 3 \times \alpha_{\rm glass} = 1.20 \times 10^{-5}\) K\(^{-1}\). From Table 1, \(\beta_{\rm Hg} = 18 \times 10^{-5}\) K\(^{-1}\), so \(\beta_{\rm Hg} > \beta_{\rm glass}\) as expected for overflow to occur.

The volume overflow is \(\Delta V_{\rm Hg} - \Delta V_{\rm glass} = V_{0} \Delta T (\beta_{\rm Hg} - \beta_{\rm glass}) = 200 \times 80 \times 16.8 \times 10^{-5}\) = 2.7 cm\(^{-3}\).